
はじめに
Kaggleは、英語のページしかありません。そこで、日本語で読みたい方向けに記事を作成しました。
Digit Recognizerの概要の説明が前の記事で済みました。
次に実際にGoogle Colabを動かしてみましょう(https://www.kaggle.com/code/yassineghouzam/introduction-to-cnn-keras-0-997-top-6を参考にして説明)。
Google Colaboratoryについては知りたい方は、以下のブログ記事を参考にしてください。
>>Google Colaboratoryとは? いつできた? mount、ファイルの読み込み等の使い方
>>Google Colaboratoryよく使う便利なショートカットキー
データのインポート
必要なものをインポートします。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import seaborn as sns
%matplotlib inlineドライブをマウントしてください。
from google.colab import drive
drive.mount('/content/drive')そして、データをインポートします。
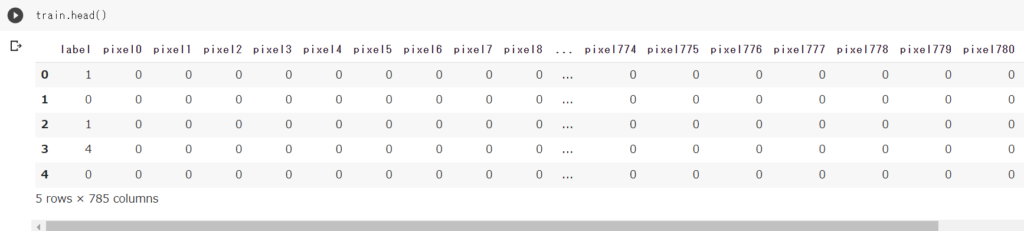
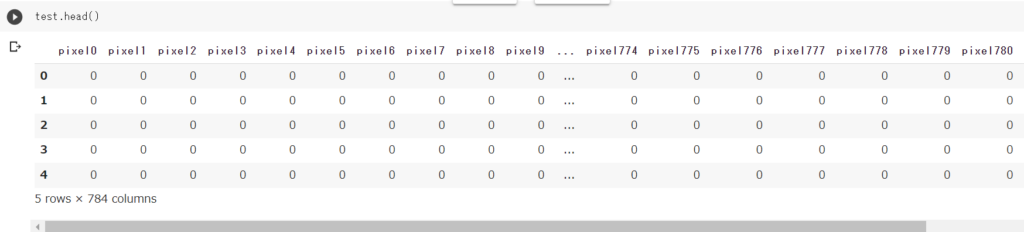
train = pd.read_csv('/content/drive/MyDrive/kaggle/Digit Recognizer/train.csv')
test = pd.read_csv('/content/drive/MyDrive/kaggle/Digit Recognizer/test.csv')注意:‘/kaggle/Digit Recognizer/train.csv’←の部分はドライブのフォルダ構成によって内容が異なるので注意してください。
EDA
まず、目的値を取り出しY_trainに格納します。
Y_train = train['label']
Y_train.head()
目的値の合計値をグラフで表示してみます。
g = sns.countplot(Y_train)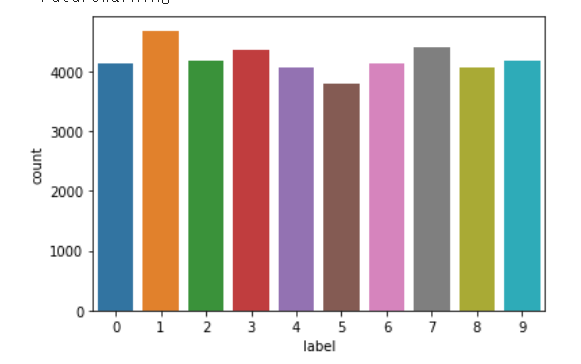
変数は 0 から 9 までの整数である。つまり、これは多クラス分類問題です。
変数0 から 9 までの整数の数をみてみます。
Y_train.value_counts()
次に、trainデータから目的値以外を取り出し、X_trainに格納します。
X_train = train.drop('label',axis=1)
X_train.head()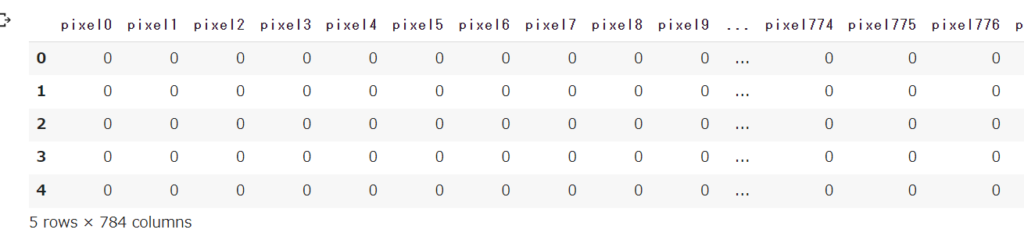
欠損値を確認します。
X_train.isnull().values.sum()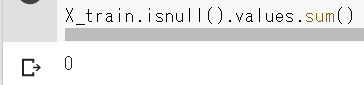
isnull()は、nanがあるとTRUEを返します。このvalues属性(numpy.ndarray)から、sum()を使うと、全体の欠損値の個数(総数)が取得できます。
testデータの欠損値も確認します。
test.isnull().values.sum()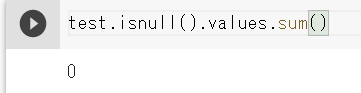
データ前処理
今回のコンペは画像分類なので、CNNを使用します。
CNNとは、Convolutional Neural Network(畳み込みニューラルネットワーク)の略です。
CNNを扱うためには、まずは画像の前処理を行う必要があります。
そもそも画像は、通常RGBカラーで表されます。つまり、Red,Green,Blueの3色です。
その3色は、それぞれ0~255の値で表されます。通常こちらを、0.0~0.1の範囲に収まるように変換する必要があります。
つまり、正規化(Normalization)を行います(データの前処理)。
ただし、今回のデータセットであるMNISTは、グレースケールです。つまり、白から灰色で表されています。
しかし、グレースケールの場合も値は0-255の値で表されており、その値に応じて白〜黒までの色を表現しています。
そこで、画像の前処理としては、通常のRGBカラーの時と同じく、変数を255で割ることでそれぞれの要素を0.0~0.1に変換する正規化を行います。
この前処理により、CNNモデルにとって、非常に処理がしやすくなりますし、精度も向上します。
X_train = X_train / 255.0
X_train.head()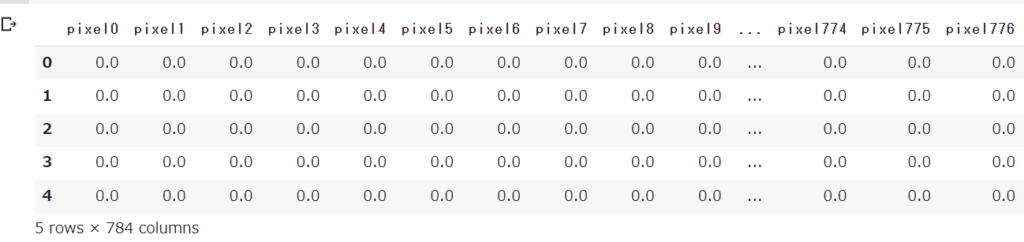
test = test / 255.0
test.head()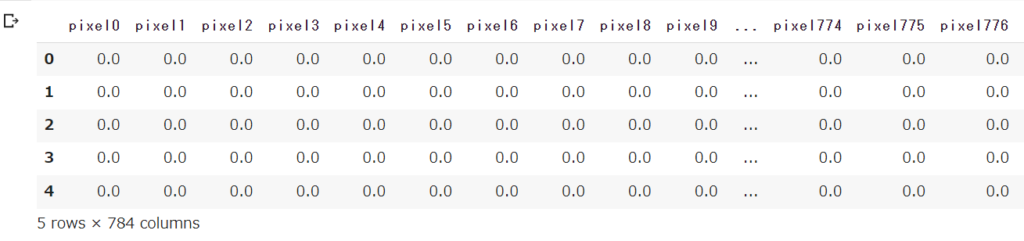
次に、データを3次元に変形します。
X_trainとtest は、784個の値からなる1次元ベクトルとしてpandas.Dataframeに格納されています。
これを28x28x1の3次元行列に整形します。
X_train = X_train.values.reshape(-1,28,28,1)
test = test.values.reshape(-1,28,28,1)ここで一つ視覚化してみましょう。
g = plt.imshow(X_train[0][:,:,0])数字の手書きの1が表示されました。
次に、label encodingを行います。
ニューラルネットワークを使用するには、特徴量をすべて数字にする必要があります。
もっとも、本コンペの目的値のlabelは、0から9までの10桁の数字です。
そこで、今回は、これらを一次元のベクトル(例:2→[0,0,1,0,0,0,0,0])に符号化します。
from keras.utils.np_utils import to_categorical
Y_train = to_categorical(Y_train, num_classes = 10)バリデーションデータを作成します。
バリデーションデータ(10%)をモデルの評価用検証セットとし、残り(90%)をモデルのトレーニングに使用します。
from sklearn.model_selection import train_test_split
random_seed =2
X_train,X_val,Y_train,Y_val = train_test_split(X_train,Y_train,test_size=0.1,random_state=random_seed)モデルの作成
モデルの作成には、ニューラルネットワークの主なライブラリであるKerasのSequential APIを使います。
Kerasは、tensorflowなどのライブラリをバックエンドとしているので扱いやすいです。
まず、畳み込み(Conv2D)層について設定します。
これは、学習可能なフィルタのセットのようなものです。最初の2つのConv2D層には32のフィルターを、最後の2つのConv2D層には64のフィルターを設定することにした。
各フィルターはカーネルフィルターを使って画像の一部(カーネルサイズで定義)を変換します。カーネルフィルターは画像全体に適用されます。
畳み込み(Conv2D)層には、relu関数(活性化関数)を使用します。relu関数(活性化関数)は、非直線性を追加するために使用します。
次に、プーリング(MaxPool2D)層を設定します。
この層は、2つの隣接するピクセルを見て、最大値を選びます。計算コストを削減し、ある程度のオーバーフィッティングを減らすために使用されます。
ここでは、プーリングサイズ(毎回プールされる領域サイズ)を選択する必要があります。
そして、ドロップアウトも設定します。
これは正則化手法の一つで、学習サンプルごとに層内のノードの一部をランダムに無視(ウェイトをゼロにする)します。これにより、ネットワークの割合がランダムに減少し、分散的に特徴を学習するようになります。また、この手法により汎化が向上し、オーバーフィッティングが減少します。
そして、Flatten層も設定します。
これは、最終的な特徴マップを1つの1次元ベクトルに変換するために使用されます。このFlatten化のステップは、畳み込み/マックスプール層の後に完全連結層を利用できるようにするために必要です。
最後の層(Dense)では、ソフトマックス関数で各クラスの確率の分布を出力しています。
これらをコードで表してみます。
from keras.models import Sequential
from keras.layers import Dense,Dropout,Flatten,Conv2D,MaxPool2D
model = Sequential()
model.add(Conv2D(filters=64,kernel_size=(3,3),padding='Same',activation='relu'))
model.add(Conv2D(filters=64,kernel_size=(3,3),padding='Same',activation='relu'))
model.add(MaxPool2D(pool_size=(2,2),strides=(2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(256,activation='relu'))
model.add(Dropout(0.5))
model.add(Dense(10,activation='softmax'))
モデルにレイヤーを追加したら、スコア関数、損失関数、および最適化アルゴリズムを設定する必要があります。
損失関数は、labelが分かっている画像に対して、モデルがどの程度うまく機能するかを測定します。これは、観察されたラベルと予測されたラベルの間のエラー率を表示しています。
本コンペは多クラス分類なので、“categorical_crossentropy “と呼ばれる特別な形式を使用します。
最も重要な機能はオプティマイザーです。この関数は、損失を最小化するために、パラメータ(フィルターカーネル値、ニューロンの重みとバイアス…)を繰り返し改善します。
RMSprop(デフォルト値)を選択しましたが、これは非常に効果的なオプティマイザーです。
このモデルの性能を評価するために、“accuracy “という評価指標を使用しました。
この評価指標は損失関数と似ていますが、その結果はモデルの学習時には使用されません(評価用のみ)。
#オプティマイザーの定義
from tensorflow.keras.optimizers import RMSprop
optimizer = RMSprop(learning_rate=0.001, rho=0.9, epsilon=1e-08, decay=0.0)*注意:kerasの前に tensorflow.をつけないとエラーがでます。
# モデルのコンパイル
model.compile(optimizer=optimizer,loss='categorical_crossentropy',metrics=['accuracy'])オプティマイザーをより速く収束させ、損失関数のグローバル・ミニマムに最も近づけるために、学習率(learning rate)のアニーリング法を使います。
損失関数のグローバル・ミニマムに効率的に到達するためには、学習率を下げることが望ましい。
Keras.callbacksのReduceLROnPlateau関数で、3エポック後に精度が改善されない場合、learning rateを半分に減らすことを選択しました。
#learning rateを設定する
from tensorflow.keras.callbacks import ReduceLROnPlateau
learning_rate_reduction = ReduceLROnPlateau(monitor='val_acc',
patience=3,
verbose=1,
factor=0.5,
min_lr=0.00001)*注意:kerasの前に tensorflow.をつけないとエラーがでます。
epochs = 1
batch_size = 86オーバーフィットを回避するために、手書き数字のデータセットを人為的に拡張する必要があります。
これは、誰かが数字を書くときに発生するバリエーションを再現するためです。 例えば、数字を中心に書かない人、大きい数字で書く人、小さい数字で書く人…などにも対応させるためです。
これらの変換をトレーニングデータに適用するだけで、トレーニングサンプルの数を簡単に2倍、3倍に増やすことができ、非常にロバストなモデルを作成することができます。この改善は重要です。
#拡張としては、4パターン行います。
#①データの補強 学習用画像の一部をランダムに10度回転させる。
#②学習用画像をランダムに10%拡大する。
#③水平方向に幅の10%分ランダムにずらす。
#④ランダムに縦方向に10%ずらす。
#vertical_flipやhorizontal_flipは、6や9のような対称的な数字の分類を誤る可能性があるため、適用しません。
from keras.preprocessing.image import ImageDataGenerator
datagen = ImageDataGenerator(
featurewise_center=False,
samplewise_center=False,
featurewise_std_normalization=False,
samplewise_std_normalization=False,
zca_whitening=False,
rotation_range=10,
zoom_range=0.1,
width_shift_range=0.1,
height_shift_range=0.1,
horizontal_flip=False,
vertical_flip=False
)
datagen.fit(X_train)モデルにフィットさせます。
history = model.fit_generator(datagen.flow(X_train,Y_train, batch_size=batch_size),
epochs = epochs, validation_data = (X_val,Y_val),
verbose = 2, steps_per_epoch=X_train.shape[0] // batch_size
, callbacks=[learning_rate_reduction])モデルを評価します。訓練と検証の損失と精度のカーブをプロットします。
fig,ax = plt.subplots(2,1)
ax[0].plot(history.history['loss'],color='b',label='training loss')
ax[0].plot(history.history['val_loss'],color='r',label='val loss')
legend = ax[0].legend(loc='best',shadow=True)
ax[1].plot(history.history['accuracy'],color='b',label='training acc')
ax[1].plot(history.history['val_accuracy'],color='r',label='val acc')
legend = ax[1].legend(loc='best',shadow=True)
Confusion matrixをみてみます。Confusion matrixはモデルの欠点を見るのに非常に有用です。
from sklearn.metrics import confusion_matrix
import itertools
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, cm[i, j],
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
Y_pred = model.predict(X_val)
Y_pred_classes = np.argmax(Y_pred,axis = 1)
Y_true = np.argmax(Y_val,axis = 1)
confusion_mtx = confusion_matrix(Y_true, Y_pred_classes)
plot_confusion_matrix(confusion_mtx, classes = range(10))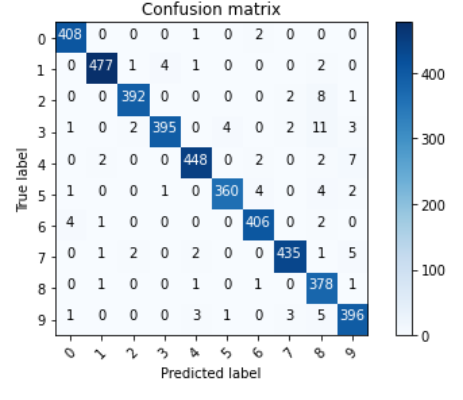
上の図のpredict labelの9の数字をみてみると、4の数字が9に多く誤分類されています。 これについて、調査してみましょう。
# エラー結果を表示。エラーは、予測されたラベルと真のラベルの差
errors = (Y_pred_classes - Y_true != 0)
Y_pred_classes_errors = Y_pred_classes[errors]
Y_pred_errors = Y_pred[errors]
Y_true_errors = Y_true[errors]
X_val_errors = X_val[errors]
## この関数は6枚の画像とその予測ラベルと実ラベルを表示
def display_errors(errors_index,img_errors,pred_errors, obs_errors):
n = 0
nrows = 2
ncols = 3
fig, ax = plt.subplots(nrows,ncols,sharex=True,sharey=True)
for row in range(nrows):
for col in range(ncols):
error = errors_index[n]
ax[row,col].imshow((img_errors[error]).reshape((28,28)))
ax[row,col].set_title("Predicted label :{}\nTrue label :{}".format(pred_errors[error],obs_errors[error]))
n += 1
## 間違った予測数値の確率
Y_pred_errors_prob = np.max(Y_pred_errors,axis = 1)
## エラーセットにおける真の値の予測される確率
true_prob_errors = np.diagonal(np.take(Y_pred_errors, Y_true_errors, axis=1))
## 予測されたラベルと真のラベルの確率の差
delta_pred_true_errors = Y_pred_errors_prob - true_prob_errors
## delta_pred_true_errorsの誤差をソートしたリスト
sorted_dela_errors = np.argsort(delta_pred_true_errors)
# Top 6 errors
most_important_errors = sorted_dela_errors[-6:]
## エラー上位6つを表示
display_errors(most_important_errors, X_val_errors, Y_pred_classes_errors, Y_true_errors)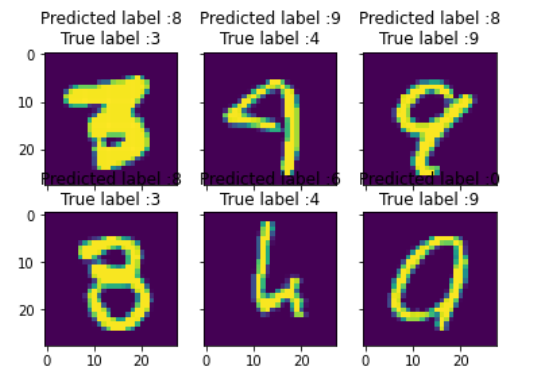
上記の6つのケースは、モデルとしておかしいものではありません。これらのエラーのいくつかは人間でも起こりうるもので、特に9は4に非常に近いです。最後の9も非常に誤解を招くもので、0にも見えます。
#予測の結果
results = model.predict(test)
results = np.argmax(results,axis = 1)
results = pd.Series(results,name="Label")ファイルの提出
submission = pd.concat([pd.Series(range(1,28001),name = "ImageId"),results],axis = 1)
submission.to_csv("submission.csv",index=False)画像分類やニューラルネットワークで悩んだら
本で画像分類について学びたい方は、「Python3年生 機械学習のしくみ 体験してわかる! 会話でまなべる!」が、内容がやさしく、わかりやすいのでオススメです。
本ではなく、動画で学びたい方は、Youtubeで公開されている予備校のノリで学ぶ「大人の数学・物理」チャンネルの「高校数学からはじめる深層学習入門(畳み込みニューラルネットワークの理解)」がオススメです。本コンペのように画像分類で使用する畳み込みニューラルネットワークで用いられる数学をわかりやすく紹介してくれています。
もっとも、動画では、深層学習の数学部分にしか触れられておらず、プログラミングは学ぶことができません。しかし、上記動画は、プログラミングスクールであるAidemy Premium Planとタイアップして作成されています。
そこで、最短距離でニューラルネットワークのプログラミングを学びたい方は、日本最大級のAI・人工知能プログラミングスクールである「Aidemy Premium Plan」の無料ビデオカウンセリングを受講してみてはいかがでしょうか。
ニューラルネットワークを学べる動画のプラットフォームとしては、キカガクもオススメです。動画の内容が非常にわかりやすく、Udemyでも大好評です。こちらも興味がございましたら、以下の無料のオンライン説明会に参加してみてはいかがでしょうか。









